Desain Pemodelan Grafik T1 kel 8 - 54411137 - Lucky Suyanti

   BAB I

PENDAHULUAN

1.1  Latar Belakang

Pada saat ini, teknologi game dan animasi terus mengalami perkembangan. Animasi atau dalam bahasa inggrisnya yaitu animate yang artinya menghidupkan, member jiwa dan menggerakkan benda mati. Animasi tersebut merupakan proses membuat suatu objek yang awalnya merupakan benda mati, dan kemudian secara berurutan disusun dalam posisi yang berbeda menjadi gamar yang hidup.

Animasi secara umum dapat didefinisikan sebagai suatu sequence gambar yang ditampilkan pada tenggang waktu tertentu agar tercipta sebuah ilusi gambar yang bergerak. Pengertian animasi pada dasarnya ialah menggerakkan objek sehingga tampak lebih dinamis. Dewasa ini, banyak software-software untuk membuat animasi, antara lain : Studio Max, Macromedia, Blender dan lain-lain.

  BAB II

Object Collision modeling in 3D

Object collision modeling(tabrakan) melibatkan banyak asumsi dan perkiraan, termasuk konsep suatu ‘impuls atau dorongan’ yang tidak terlalu jelas. Hal tersebut akan kami diskusikan pada materi 3D object collision modeling.

Salah satu hal yang sulit pada collision modeling adalah memahami bagaimana suatu objek bekerja dengan objek lain yang memiliki gerakan rotasi dan linier. Metode utama yang akan kita gunakan untuk melakukan ini melibatkan beberapa tahap, antara lain :

1.      Menentukan titik tabrakan dan arah normal pada titik ini.

2.      Menghitung impuls atau dorongan minimum untuk mencegah objek berpotongan atau untuk membalik kecepatan, tergantung pada koefisien friksi.

3.      Menghitung efek impuls ini pada gerakan rotasi dan linier secara terpisah.

Hasil untuk kasus 3D ini kami rangkum sebagai berikut:

 

Keterangan :

ARAH

Ketika kita mengerjakan persamaan ini secara manual, terlihat cukup mudah untuk menentukan arah impuls dan tanda pada istilah-istilah di atas. Tapi karena ini bagian dari program komputer, maka sangatlah penting untuk memahami ketentuan yang kita asumsikan dan untuk mendapatkan tanda yang benar.

Pada diagram berikut ini, anak panah mengindikasikan arah positif, bukan kecepatan absolut yang mungkin saja arah negatif.

Dalam hal ini, v_ai> v_bi sebelum tabrakan dan v_af<= v_bf setelah tabrakan. Jadi, impuls mengurangi momentum dari objek a dan menambahkannya ke objek b sehingga kita mendapatkan rumusannya sebagai berikut:

v_af = v_ai - J/Ma

v_bf =v_bi + J/Mb

Sekarang kita membalik ukuran objek a dan objek b

 

Dalam kasus ini, v_bi> v_ai sebelum tabrakan dan v_bf <= v_af setelah tabrakan. Jadi, impuls mengurangi momentum dari objek b dan menambahkannya ke objek a sehingga kita mendapat rumusannya sebagai berikut:

v_af = v_ai + J/Ma

v_bf =v_bi - J/Mb

Sekarang tampaknya kurang efektif/kacau untuk mendapatkan program untuk menguji yang mana kecepatan tertinggi dan menentukan persamaan mana yang akan digunakan, sehingga akan lebih mudah menggunakan J negatif untuk mengindikasikan kasus kedua. Jika kamu melakukan ini, perhatikan bahwa J negatif tidak berarti ia menarik, bukan mendorong. Itu hanya berarti bahwa objek-objek bertabrakan pada arah yang lain.

Rotasi Arah

Hal tersebut akan menjadi lebih rumit dengan adanya rotasi dalam momentum angular(sudut) yang harus diukur relatif dahulu terhadap titik tertentu. Jika objek ‘a’ berputar searah jarum jam pada pusat massanya, mungkin ia memberikan momentum berlawanan arah jarum jam pada objek ‘b’ pada pusat massanya. Namun, hal ini tidak akan mengubah momentum angular dari keseluruhan sistem, bahkan untuk suatu sistem tertutup, dikarenakan   gerakan linier dari pusat massa yang berbeda. 

Kecepatan pada titik tabrakan objek ‘a’ =  VPA = VCA + ωa × (r-pa)

Kecepatan pada titik tabrakan objek ‘b’ =  VPB = VCB + ωb × (r-pb)

Derivasi (Penurunan)

Pada kasus 1D, kita dapat memulai dengan definisi koefisien restitusi yang merupakan rasio kecepatan bertemu dan memencar.

Namun, dalam kasus ini, kecepatan bukanlah kecepatan dari pusat massa, melainkan kecepatan suatu titik (pada koordinat absolut) dari suatu benda padat. Inilah yang merupakan titik-titik pada suatu benda yang sebenarnya bertubrukan.

e = (v_af- v_bf) / (v_ai - v_bi)

dimana		definisi lain
Simbol	Unit	Jenis	Unit
vcaf	kecepatan akhir titik tubrukan pada objek a	vektor	m/s
vcai	kecepatan awal titik tubrukan pada objek a	vektor	m/s
vcbf	kecepatan akhir titik tubrukan pada objek b	vektor	m/s
vcbi	kecepatan awal titik tubrukan pada objek a	vektor	m/s
e	koefisien restitusi yang bergantung pada natur dua materi yang bertubrukan	skalar	Tidak ada

Δvc_a = vc_ai - vc_af

Ini merupakan perubahan kecepatan titik tabrakan pada benda ‘a’ yang disebabkan oleh impuls.

Δvc_b = vc_bi - vc_bf

Ini merupakan perubahan kecepatan titik tabrakan pada benda ‘b’ yang disebabkan oleh impuls.

  Sehingga didapatkan :

e * (vcai - vcbi)= -(vcaf- vcbf)

(e+1) * (vcai - vcbi)= -(vcaf- vcbf)+(vcai - vcbi)

(e+1) * (vcai - vcbi)= Δvca + Δvcb

Dari relasi Δvc_a dan Δvc_b dengan impuls (J)  maka kita mendapatkan:

ΔVp = J/M + ([I]-1(J × r)) × r

dimana		definisi lain
simbol	deskripsi	jenis		Unit
Vp	Kecepatan linier suatu partikel pada benda padat (vektor)	vektor		m/s
J	Impulse		Vektor
I	skalar inersia seperti torsi = I * alpha (benar hanya jika objek simetris)		Skalar
[I]	inersia tensor		matriks 3×3
m	massa	skalar		Kg
•		• = produk dot
×		× = produk cross
r	posisi partikel relatif terhadap pusat massa – NB: ini berada pada koordinat absolut, bukan koordinat benda lokalsehingga ini menjadi fungsi waktu jika benda berotasi.		Vektor

Sehingga kita mendapatkan:

(e+1) * (vai - vbi)= J/Ma +([Ia]-1(J × ra)) x ra + J/Mb +([Ib]-1(J × rb)) x rb

Kita ingin memecahkan persamaan di atas untuk mendapatkan J. Untuk melakukannya, kita perlu memisahkan J ke bagian kanan. Arah impuls akan bergantung pada natur material yang bertubrukan dan koefisien friksinya. Jika friksi tinggi, impuls akan berada di arah yang mendatangi titik tubrukan. Jika friksi rendah, impuls akan tegak lurus terhadap permukaan tubrukan. Tidak ada impuls yang parallel terhadap permukaan karena mereka dapat tergelincir di arah tersebut. Jadi, memisahkan impuls dalam besaran dan arah dapat membuat friksi diperhitungkan dan memungkinkan besaran impuls dikeluarkan dari sisi kanan sebagai istilah biasa.

J = n*|J|

dimana			definisi lain
simbol	deskripsi		jenis	Unit
n		vektor normal yang memberikan arah impuls	Vektor
J		vektor impuls	Vektor
|J|		besaran impuls	Skalar

Dengan asumsi bahwa ada solusi yang perlu kita buat

([Ia]^-1(J × ra)) × ra = |J| * ([Ia]^-1(n × ra)) × ra

Maka Hasilnya adalah:

|J| = (e+1) * (v_ai - v_bi) / (1/Ma +n•([Ia]^-1(n × ra)) x ra + 1/Mb +n•([Ib]^-1(n × rb)) × rb)

 Kode

Metode Alternatif Menggunakan Matriks

Ide yang bagus untuk mengekspresikan semua istilah ialah dengan menggunakan jenis aljabar yang sama. Tidak mungkin mengekspresikan inersia tensor secara murni dalam istilah vektor atau quaternion. Dalam hal ini apakah mungkin kita bisa menghitung murni dalam term matriks?

Relasi antara impuls J dan perubahan kecepatan titik dimana J diterapkan, diperoleh di bawah ini:

Perubahan kecepatan linier suatu titik pada benda padat yang disebabkan

J = J/M + ([I]^-1(J × r)) × r

dimana		definisi lain
simbol	deskripsi	jenis	Unit
ixx to izz		elemen dari inersia tensor (pada koordinat absolut)
rx,ry and rz

Maka  kita dapat menyimpulkan efek J terhadap kecepatan relatif benda A dan B:

Perubahan kecepatan relatif linier dari titik tabrakan yang disebabkan J = (e+1) * (v_ai – v_bi)

Oleh karena itu, kita perlu menginvert maktriks ini untuk mendapatkan ekspresi J dalam term kecepatan approach.

Metode Lainnya

·         Solusi dengan impuls

·         tabrakan inelastis sempurna

·         tabrakan elastis sempurna

·         Solusi dengan konservasi momentum dan energi

Solusi dengan Impuls

Impuls yang ditransfer antarobjek = [NEMa]* (v_af - v_ai)= -[NEMb]*(v_bf - v_bi) dimana:

·         [NEMa] = Matriks Newton-Euler untuk objek a; ini merupakan matriks 6x6.

·         [NEMb] = Matriks Newton-Euler untuk objek b; ini merupakan matriks 6x6.

·         v_af= kecepatan akhir objek a. Ini merupakan vektor 6 dimensi yang mengandung komponen-komponen linier dan rotasi di semua 3 dimensi.

·         v_ai= kecepatan awal objek a. Ini merupakan vektor 6 dimensi yang mengandung komponen-komponen linier dan rotasi di semua 3 dimensi.

·         v_bf= kecepatan akhir objek b. Ini merupakan vektor 6 dimensi yang mengandung komponen-komponen linier dan rotasi di semua 3 dimensi.

·         v_bi= kecepatan awal objek b. Ini merupakan vektor 6 dimensi yang mengandung komponen-komponen linier dan rotasi di semua 3 dimensi.

Catatan : Saya mengasumsikan bahwa pada kasus elastis, hanya bagian linier impuls yang ditransfer antarobjek. Oleh karena itu, torsi eksternal selalu nol sehingga persamaan di atas menjadi benar. Pada kasus inelastis,  mungkin ada impuls rotasi yang ditransfer.
Satu-satunya situasi yang dapat saya pikirkan dimana impuls rotasi akan muncul adalah saat terjadi tubrukan dua massa yang berotasi pada ulir sekrup yang sama. Adakah yang dapat membantu saya mengklarifikasi hal ini? Apakah kita perlu mempertimbangkan komponen impuls rotasi pada tubrukan objek padat yang mengambang bebas?

Tabrakan inelastis sempurna

Pertama-tama kita mengambil kasus tabrakan inelastis sempurna (dimana objek saling menempel setelah tabrakan) dan kecepatan akhir mereka sama. Jadi, 

vaf= vbf (ini tidak sepenuhnya benar karena ketika objek saling menempel, mereka akan mulai saling mengitari satu sama lain, tetapi mereka akan memiliki kecepatan rata-rata yang sama dimana kecepatan ini merupakan kecepatan pusat massa)

[NEMa]* (vaf - vai)= -[NEMb]*(vbf - vbi)

Bila vaf disubstitusi dengan vbf maka:

[NEMa]* (vaf - vai)= [NEMb]*(-vaf+vbi)

Kita ingin menemukan nilai dari vaf.Saat mengalikan maktriks suatu vektor, perkalian lebih distributif dibandingkan penambahan sehingga

[NEMa]* vaf- [NEMa]*vai=[NEMb]*vbi- [NEMb]*vaf

Kita dapat menyusun ulang vektor ini untuk mendapatkan:

[NEMa]* vaf+ [NEMb]*vaf = [NEMb]*vbi + [NEMa]*vai

Kami tidak tahu banyak tentang matriks aljabar untuk memprosesnya lebih jauh, sehingga kami akan menjabarkannya demikian: 

Mungkin ada suatu jalan dimana kita dapat menggantikan dua matriks pada bagian kiri persamaan dengan suatu matriks tunggal yang merepresentasikan inersia atau massa dari objek yang bergabung. Ini juga merupakan masalah pada bagian awal dimana dua objek saling mengitari satu sama lain sehingga memiliki matriks inersia atau massa yang berbeda. Jadi, didapatkan :

[NEMcombined]* v_af = [NEMb]*v_bi + [NEMa]*v_ai

Maka solusinya adalah:

vaf= vbf =[NEMcombined]inverse * ( [NEMb]*vbi + [NEMa]*vai )

Nilai dari impuls adalah:

impulse = [NEMa]* (vaf - vai)

impulse = [NEMa]* ([NEMcombined]inverse* ( [NEMb]*vbi + [NEMa]*vai ) - vai)

Tubrukan elastis sempurna

Pada kasus ini, diasumsikan bahwa persamaan impuls sama dengan kasus inelastis (tetapi nilainya menjadi dua kali lipat sebab objek-objek yang terpisah pada kecepatan yang sama). 

Saya tidak berpikir bahwa ini merupakan kasus yang tepat sebab pada kasus 3D tanpa friksi, impuls seharusnya normal terhadap permukaan tubrukan dan impuls rotasi seharusnya nol. Apakah ada yang dapat memberikan ide bagaimana menghitung nilai impuls ini?

impulse = 2 [NEMa]* ([NEMcombined]inverse * ( [NEMb]*vbi + [NEMa]*vai ) - vai)

Kecepatan akhir = kecepatan awal + impuls

vaf= vai + 2 [NEMa]* ([NEMcombined]inverse * ( [NEMb]*vbi + [NEMa]*vai ) - vai)

Solusi dengan konservasi momentum dan energy

Dengan konservasi momentum linier:

Dengan konservasi momentum angular:

dimana semua rotasi pada persamaan di atas hampir sama seperti pada kasus 2D. Jika kita ingin mengukur rotasi objek itu sendiri pada pusat massanya, kita perlu menerapkan teorema sumbu paralel dimana akan menambah variable lain pada persamaan di atas.

Dengan konservasi energi

Ini menghasilkan 7 persamaan dengan 12 variabel yang tidak diketahui sehingga kita membutuhkan informasi tambahan untuk memecahkannya:

·         kecepatan a : v_afx, v_afy, dan v_afz

·         kecepatan b : v_bfx, v_bfy, dan v_bfz

·         rotasi a terhadap sumbu x : wax

·         rotasi a terhadap sumby y : way

·         rotasi a terhadap sumbu z : waz

·         rotasi b terhadap sumbu x : wbx

·         rotasi b terhadap sumby y : wby

·         rotasi b terhadap sumbu z : wbz

Jadi, ada ketidakcukupan informasi untuk memecahkan persamaan ini sehingga kita perlu menambah informasi tambahan seperti batasan-batasan yang dapat diterapkan atau penerapan ‘sudut insidensi = sudut pencerminan’.

Walaupun kita memiliki informasi yang cukup untuk memecahkan kasus umum, persamaan tersebut masih sangat rumit untuk dapat dipecahkan dalam kasus umum. Khususnya karena kita tidak bekerja dalam frame-of-reference dari bentuk-bentuk individual, maka secara umum variabel I (Inersia) merupakan suatu fungsi sudut-sudut objek. Gerakan rotasi objek membuat persamaan tersebut menjadi semakin rumit sehingga kita perlu menggunakan pendekatan yang berbeda seperti berikut:

Asumsikan bahwa kita bergerak ke frame referensi bentuk 1, maka bentuk 1 akan selalu muncul stasioner pada frame ini. Pergerakan bentuk 2 akan lebih mudah dihitung pada frame ini, misalnya jika kita mengasumsikan bahwa impuls berada pada arah normal saja (tidak ada pergeseran). Oleh karena itu, pergerakan paralelnya terhadap bidang datar akan konstan dan pergerakan normalnya terhadap bidang datar akan terbalik selama tabrakan. Mungkin ada energi yang ditransfer antara pergerakan linier dan angular, bergantung pada  posisi relatif pusat massa bentuk 2 dan titik tabrakan, namun sebagai perkiraan pertama, apakah mungkin kita mengabaikan hal tersebut?

Kita masih harus menghitung bagaimana pergerakan frame-of-reference telah berubah selama tabrakan, tetapi ini relatif mudah menggunakan konservasi momentum.

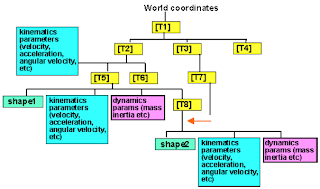
Jadi, bagaimana memindahkan bentuk 1 ke ­frame-of-reference? Yang harus kita lakukan adalah memindahkan bentuk 2 di bawah bentuk 1 pada scene graph, jangan lupa terjemahkan semua parameter yang terkait dengan bentuk.

Jadi, transform [T8] memberikan posisi bentuk 2 relatif terhadap bentuk 1 dimana dalam kasus ini:

[T8] = [T7][T3][inverse T2][inverse T5]

Jangan lupa kita harus mentransform semua parameter kinematis dan dinamis untuk bentuk 2.

Komponen Rotasi untuk contoh 3D di atas

Jika kita mengasumsikan bahwa kedua objek menjelajahi ruang bebas (tidak ada torsi eksternal), ketika mereka bertabrakan maka mereka akan menjelajahi ruang bebas lagi.

Seperti dijelaskan di atas, rotasi awal diketahui dan kita ingin menentukan rotasi akhir. Pada saat tubrukan, energi dapat ditransfer antara objek-objek yang bertabrakan dan antara energi linier dan rotasi.

Hukum konservasi momentum dan energi di atas tidak cukup untuk menentukan kecepatan akhir. Kita perlu mencari faktor lain yang ditentukan oleh geometri objek.

Salah satu faktor adalah objek-objek hanya dapat berotasi pada sumbu tertentu (tidak ada torsi). Jika objek merupakan suatu bulatan sempurna (atau minimal variable inersianya sama di semua arah), objek dapat berotasi pada semua arah, namun minimal kita adapat menggunakan bentuk simetrisnya untuk menyederhanakan persamaan. Jika objek tidak simetris, mereka hanya dapat berotasi pada sumbu tertentu dimana ini akan membatasi hasil yang diharapkan.

Faktor lainnya adalah posisi titik dampak relatif terhadap pusat massa dua objek.

Jika ini terlalu rumit, kamu dapat mempertimbangkan pendekatan numeris lainnya terkait dengan tabrakan.

Minutes of meeting